全同态加密 Fully homomorphic encryption (FHE)

What’s is FHE

第一种形式：同时使用secret key加密和解密，public key用于第三方加密进行同态计算

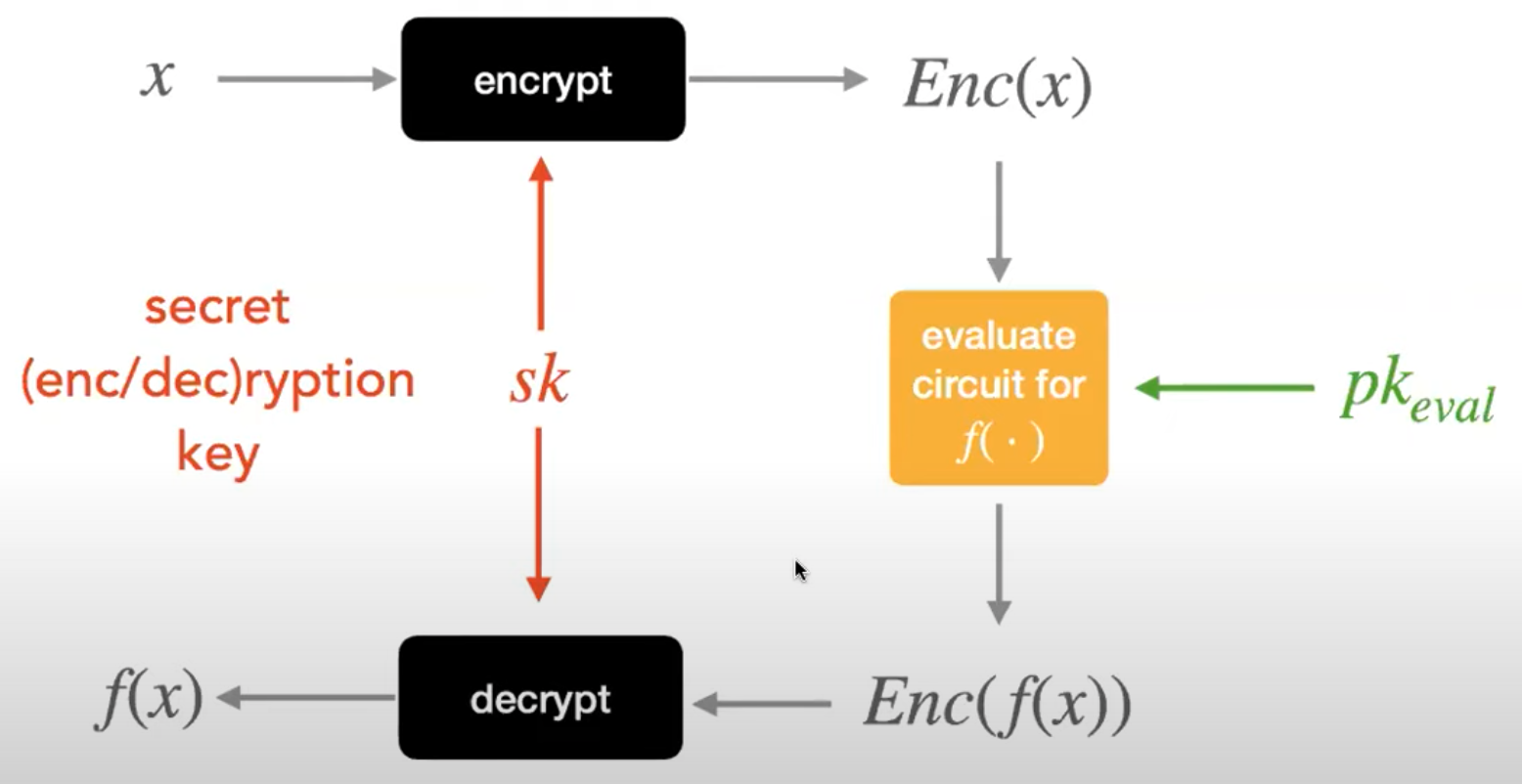
第二种形式：asymmetric FHE，只使用public key进行加密，secret key用于解密

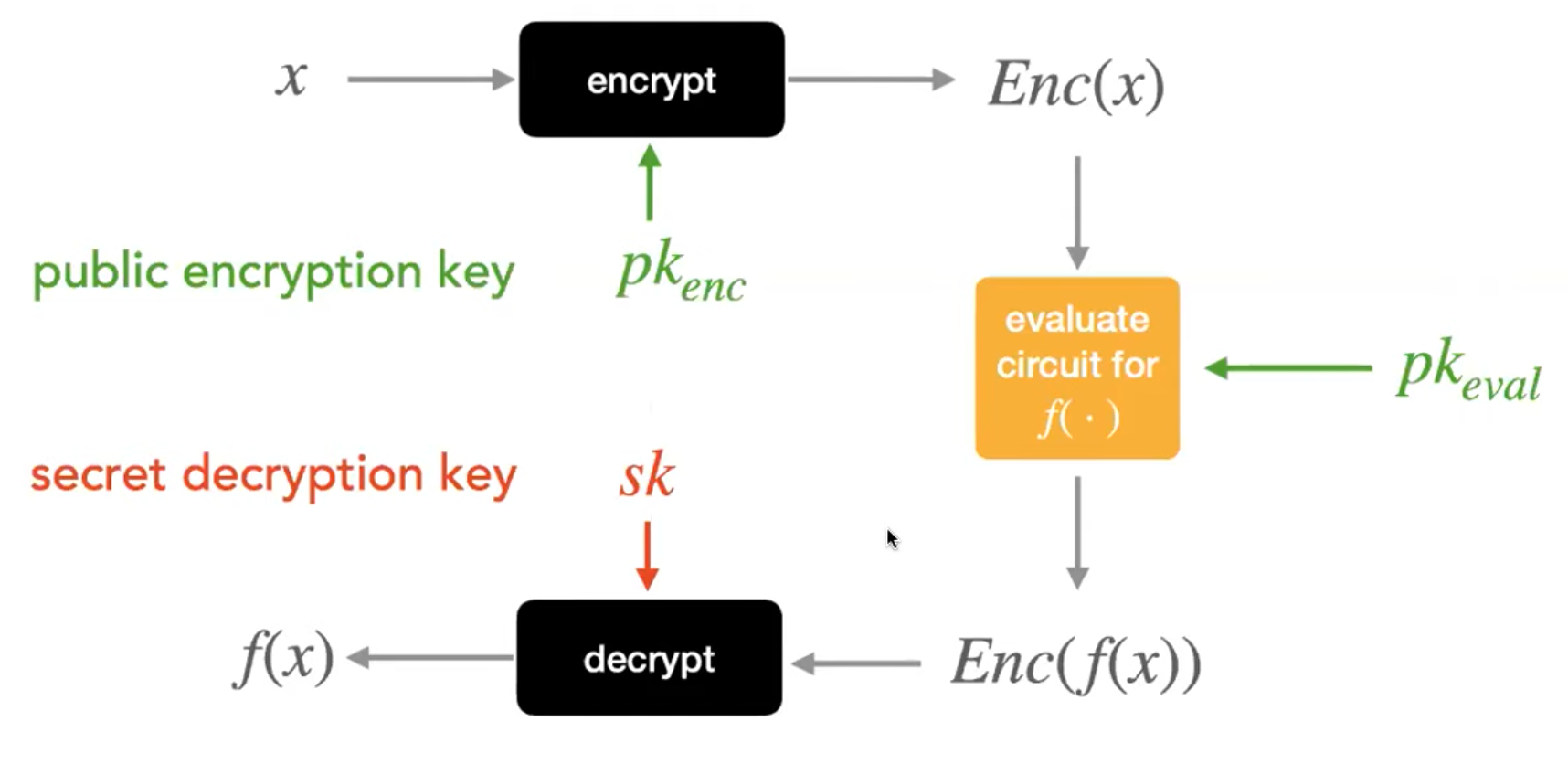
Efficient FHE is a giant leap towards httpz://

? what’s httpz?

History

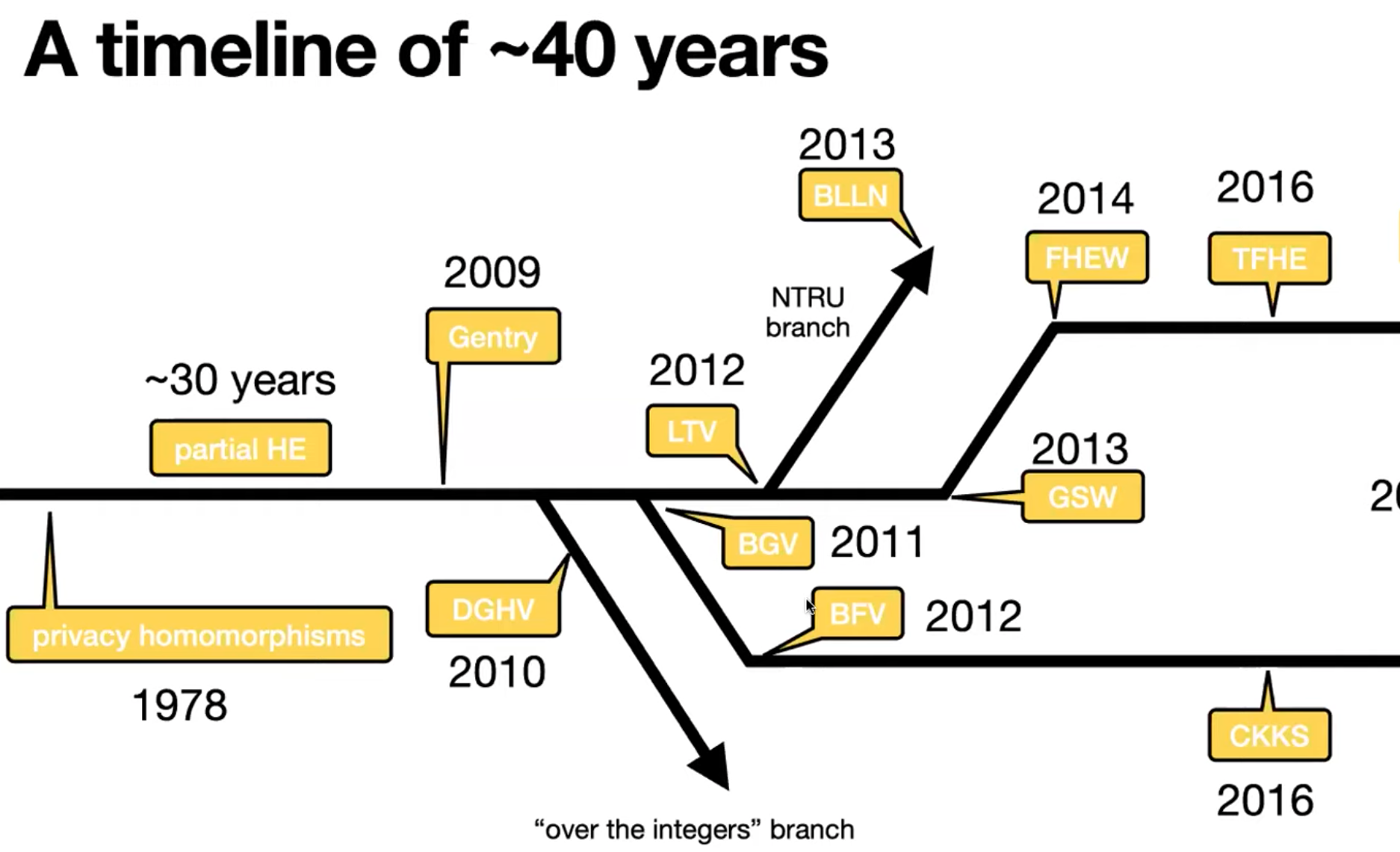
Major task: find a new scheme to combine both addition and multiplication together.

1. First generation

Plain text: single bit

After installing PyG, here is the error:

libc10_cuda.so: cannot open shared object file: No such file or directory

Solution

1
2

conda install pytorch==1.11.0 cudatoolkit=11.3 -c pytorch
conda install pyg -c pyg

在运行任务时，往linux的同一个文件夹中写入超过500万个文件，导致在硬盘还有空间的情况下，在该文件夹下无法继续写入文件，也无法使用ls、rm等命令。记录处理过程。

Background: physical server, about two years old, 7200-RPM SATA drives connected to a 3Ware RAID card, ext3 FS mounted noatime and data=ordered, not under crazy load, kernel 2.6.18-92.1.22.el5, uptime 545 days. Directory doesn’t contain any subdirectories, just millions of small (~100 byte) files, with some larger (a few KB) ones.

We have a server that has gone a bit cuckoo over the course of the last few months, but we only noticed it the other day when it started being unable to write to a directory due to it containing too many files. Specifically, it started throwing this error in /var/log/messages:

Automatically Sort Data in Google Sheets

Extension -> Apps script

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

function autoSort(e) {
  const ss = SpreadsheetApp.getActiveSpreadsheet()
  const ws = ss.getSheetByName("Sheet1")
  const range = ws.getRange(2,1,ws.getLastRow()-1,2)
  range.sort({column: 2, ascending: false})
}

function onEdit(e){
  autoSort(e)
}

1. Check SWAP used by differnt PID

1

for i in $(cd /proc;ls | grep "^[0-9]" | awk '$0>100'); do awk '/Swap:/{a=a+$2}END{print '"$i"',a/1024"M"}' /proc/$i/smaps;done| sort -k2nr | head

2. Get the information about the PID

1

ps aux | grep ${pid}

显示“未能找到金属编译器安装的Xcode。请安装Xcode并运行Xcode.app来接受协议，或确保激活的开发者目录设为当前的Xcode安装（使用xcode-select）

解决方案：

1

sudo xcode-select -s /Applications/Xcode.app/Contents/Developer